Conical sundials
In ancient Greece, measuring time with sundials on sunny days was an integral part of everyday life. Several sculptured sundials of various types, mostly conical, have survived to the present day and are preserved in the country’s archaeological museums.
Sundials are made up of the dial plateon which lines (hour lines) and curves are inscribed and the gnomon. The time of day and season are determined by the shadow of the sun cast by the gnomon on the dial plate. The position of the shadow in relation to the hour lines gives the time of day and the relation of the shadow’s position to the curves gives the time of year.
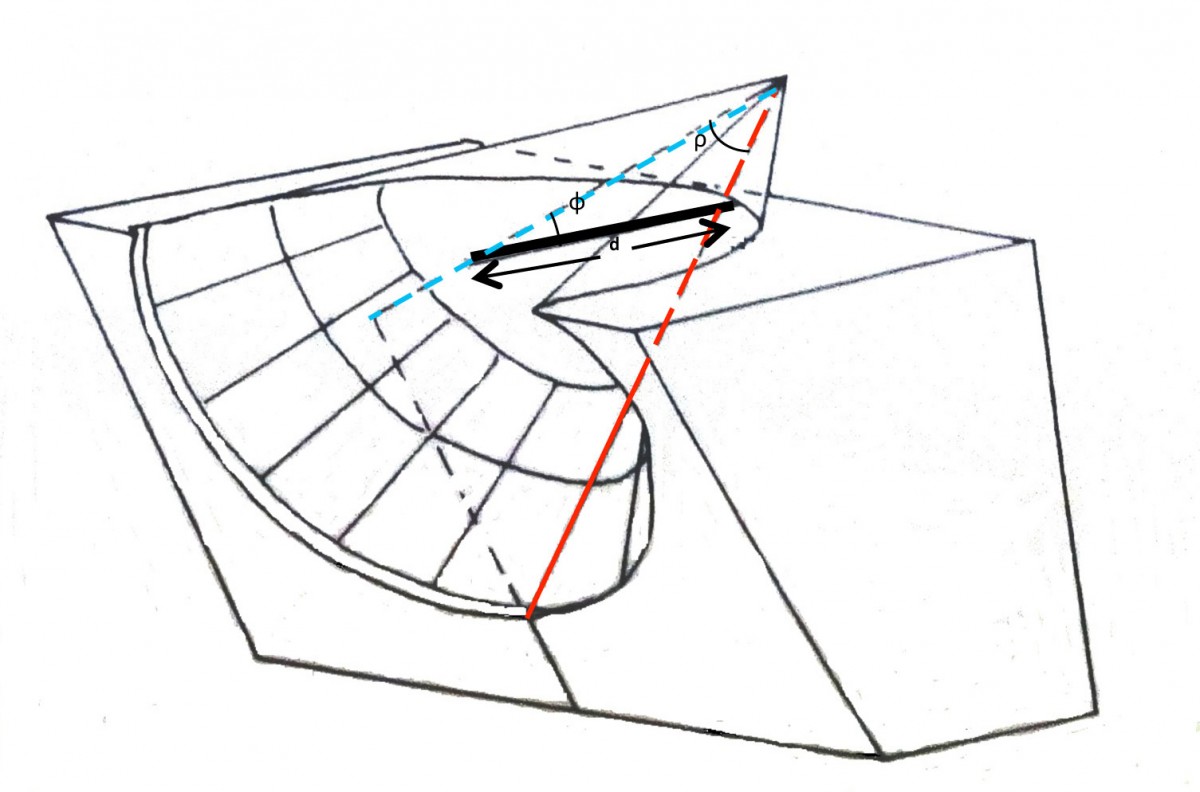
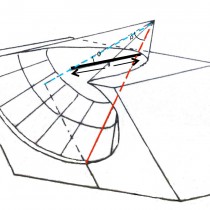
A feature of conical sundials is the shape of their dial plate which is part of a conical surface with an axis parallel to that of the Earth. Essentially, the conical surface shows an incline in relation to the horizontal surface equal to the angle formed by the celestial equator with the horizon of the country. Eleven hour lines are inscribed on the dial plate of conical sundials that intersect with the curves of the winter solstice, summer solstice and equinoxes. The hour lines and day curves of conical sundials create a network of lines that have been approximated with considerable precision with arcs of conic sections that join corresponding hour points (Gibbs 1976: 31). The shape of the network depends on the position of the cone’s apex, the conical surface and the position of the gnomon’s base.
When analyzing the network of lines on a conical sundial, parameters φ, ρ and d can be measured:
φ is the geographic latitude of the place the sundial is positioned.
ρ is the angle between the cone’s axis and the generator of the sundial’s surface.
d is the length of the gnomon.
Consequently, when the above parameters are known, a conical sundial can be described and constructed.
The sundial with a gnomon in the Archaeological Museum of Piraeus
An Ancient Greek conical type of sundial with a gnomon is in the National Archaeological Museum of Piraeus, with the serial index number ΜΠ 1131.
The sundial belongs to the Roman period (Schaldach 2006: 124). In September 2013 it was displayed to the public for the first time in a temporary exhibition entitled “Light and Shade measure Time”, organized by the Museum as part of its activities. It was accompanied by lectures and educational programmes on instruments used for astronomy and measuring time in the ancient world, as well on the philosophical approach to the concept of time.
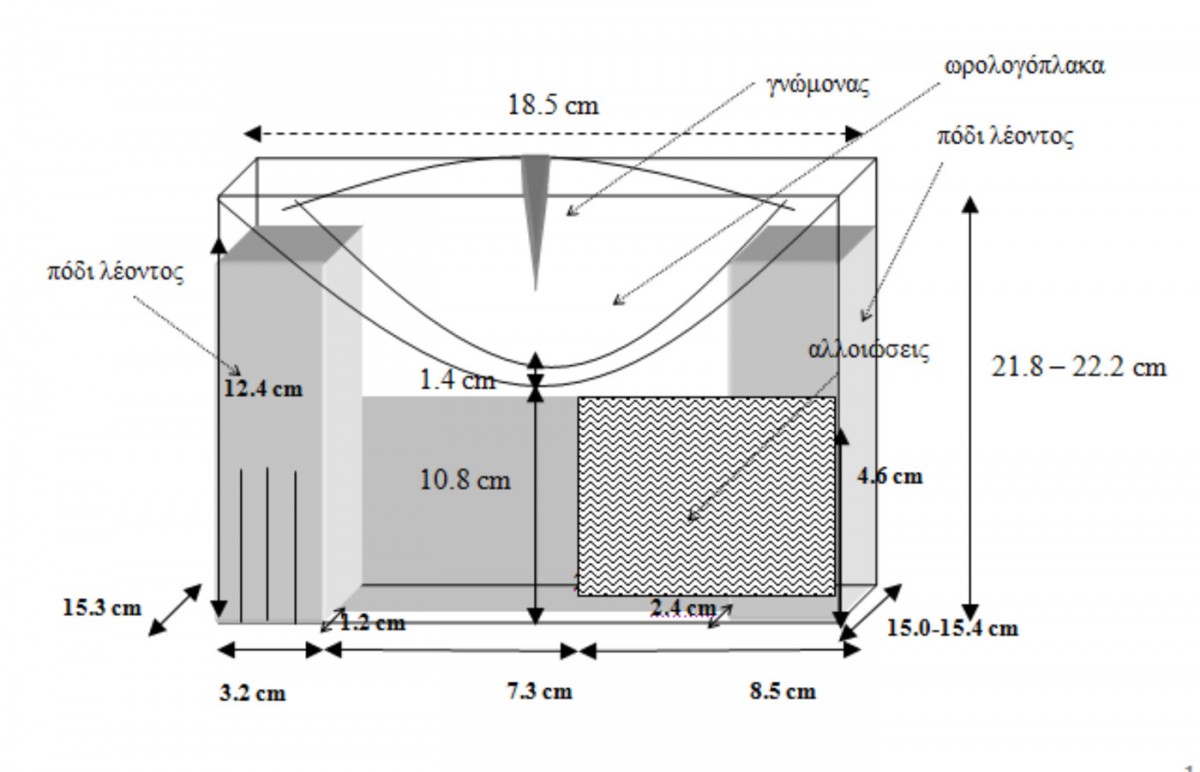
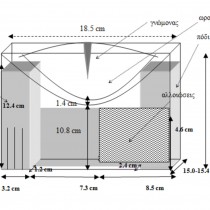
The sundial is made of marble, incorporated in a marble base with lion feet and weighs 13 kilos. Its height is between 21.8 and 22.2cm. Its depth on the dial plate’s right side is 15-15.4 cm, while on the left it is 15.3 cm. Its width on the front is 19 cm and 18.5 cm on the back.
There are visible damages on the back left corner of the marble sundial and a small part of it is also missing.
To the left and right of the sundial’s base are lion’s feet. The foot on the left side is 12.4 cm high x 3.2 cm wide x 1.2 cm deep. The right hand foot is very damaged and a 4.6 cm high marble piece is missing, with a conic section which is 8.5 cm wide by 2.4 cm deep. The distance between the bottom part of the base to the lowest point of the dial plate is 10.8 cm.
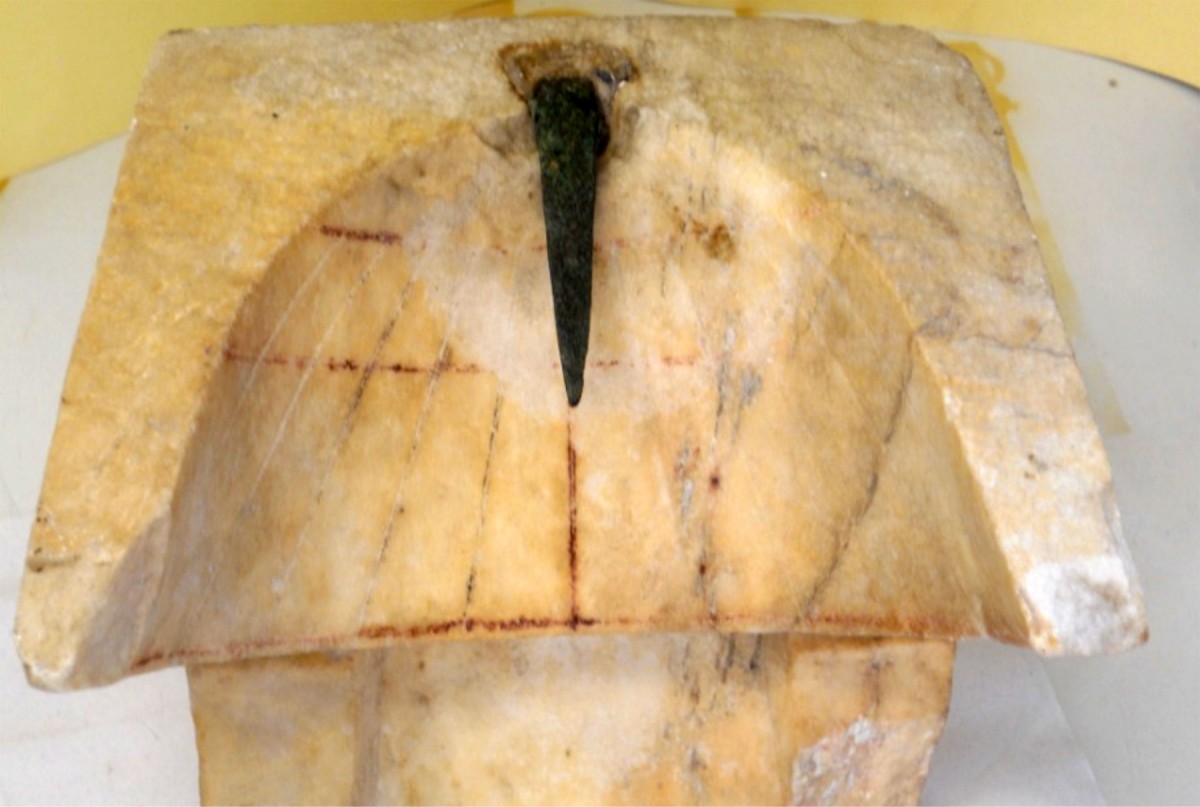
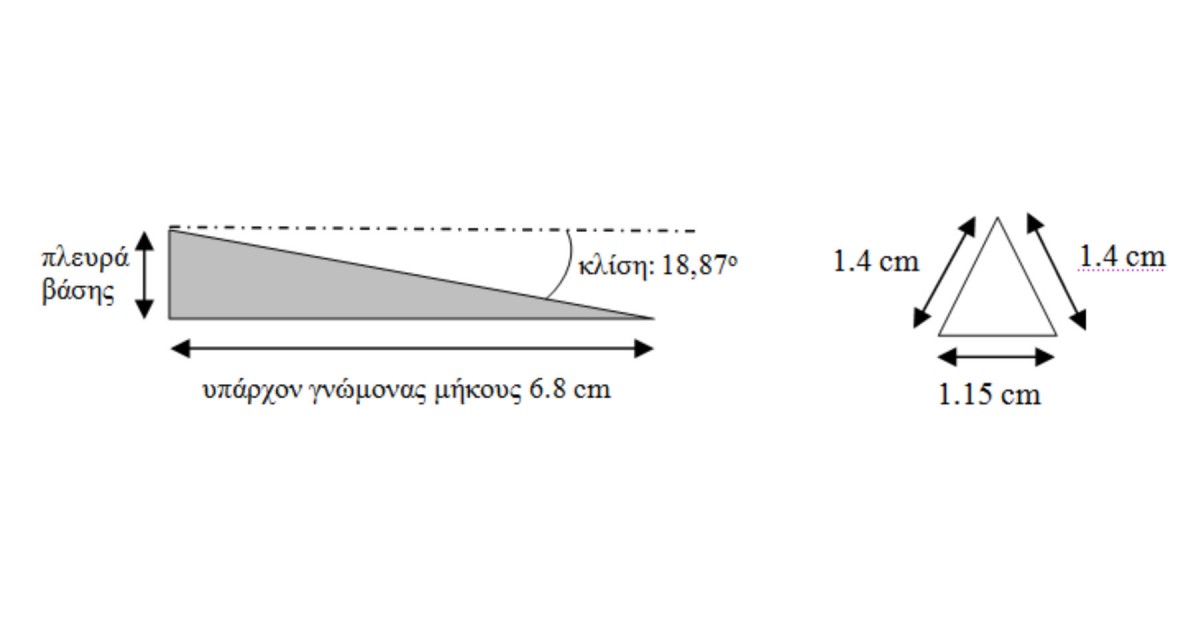
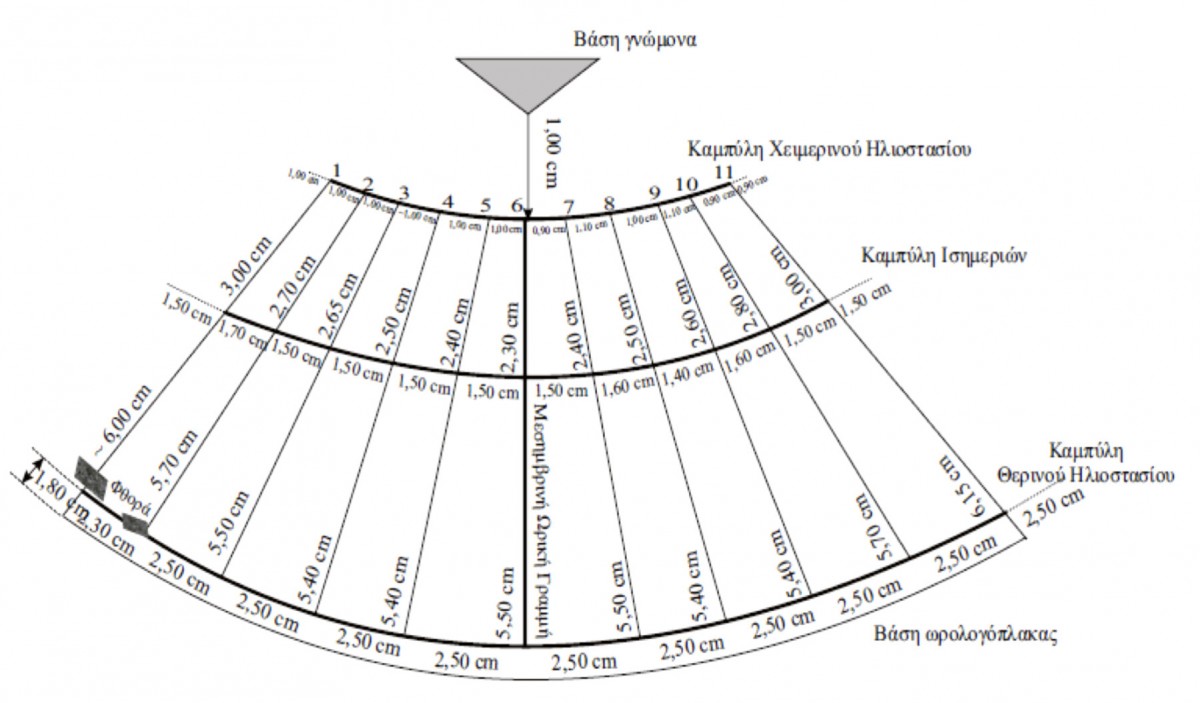
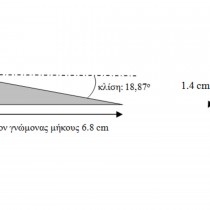
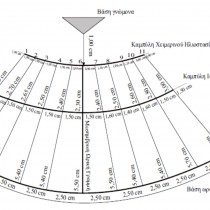
The 1.4 cm thick dial plate is very well preserved. The 11 hour lines are visible on its surface, as are the curves of the summer solstice, winter solstice and equinoxes. The curves show traces of red that are more pronounced along the sections of the curves intersecting between the 1st and the 6th hour line. There are also visible traces of red on the 6th hour (meridian) line. The damages on the dial plate are pronounced and particularly wide spread after the 7th hour line without, however, these damages completely covering the grooves of the hour lines. The sundial’s horizontal gnomon has survived and visibly slants in relation to the horizon level. It is made of brass (bronze), shaped like a pyramid with a triangular base and measures 1.4×1.4×1.15 cm. The gnomon’s current length is 6.80 cm.
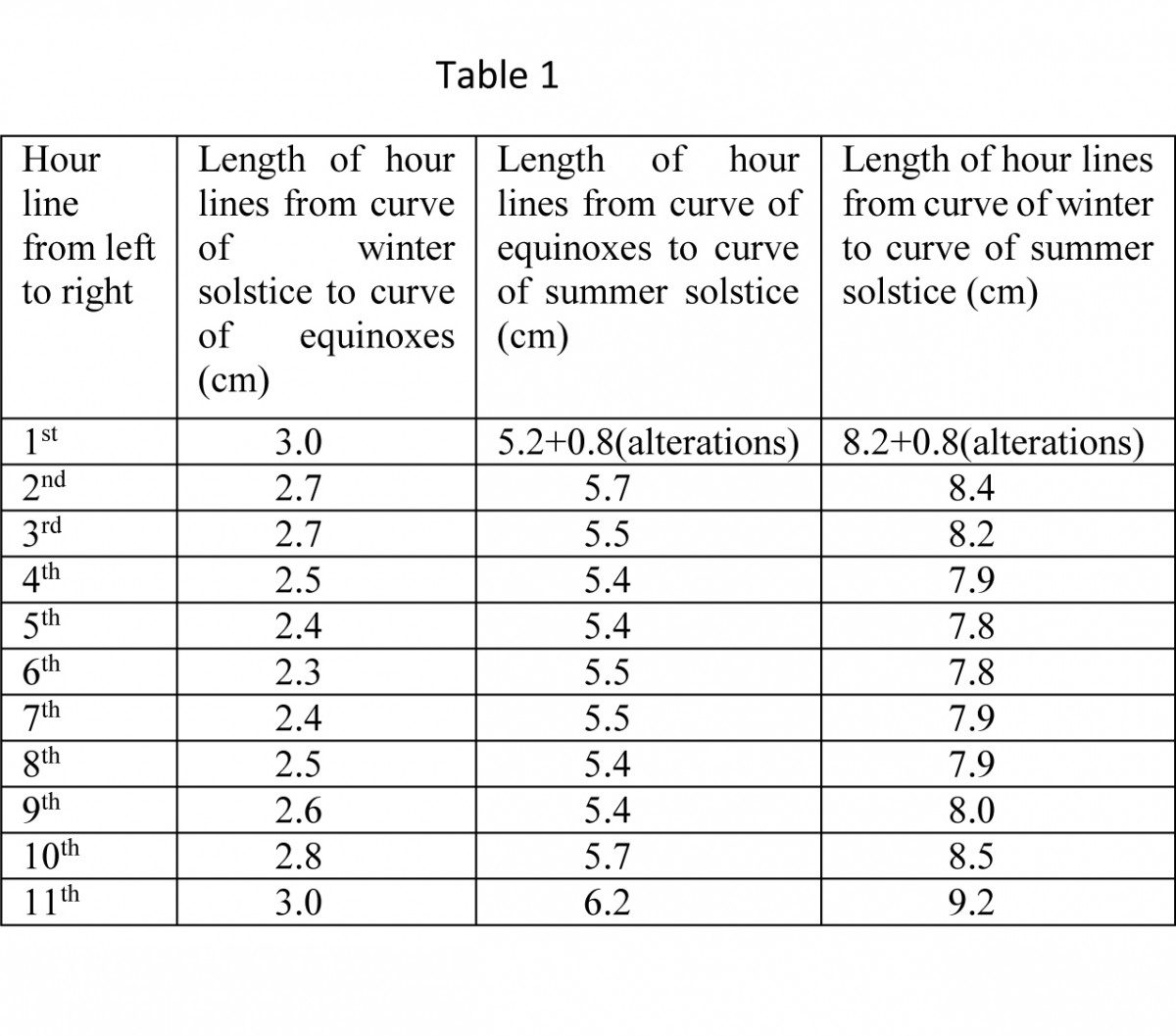
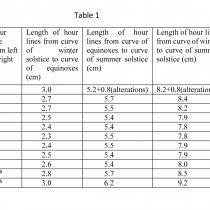
Listed in Table 1 are the lengths of the hour lines (from left to right) from the curve of the winter solstice to the curve of the equinoxes and from the curve of the equinoxes to the curve of the summer solstice.
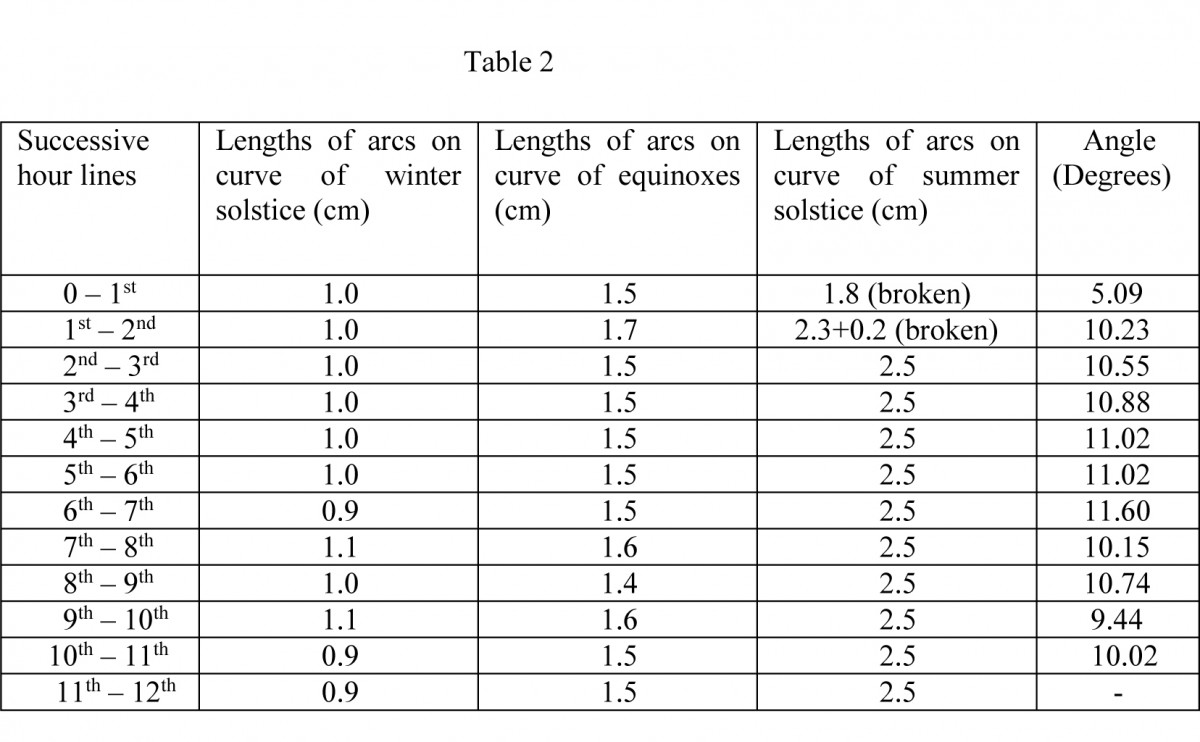
Listed in Table 2 are the lengths of the arcs formed in succession on the curve of the winter and summer solstices and equinoxes by the intersection of the hour lines with these curves. Also listed are the calculated values of the angles formed between the successive hour lines. The angles formed by the successive hour lines for the afternoon hours are not symmetrical with the corresponding morning ones in regards to the meridian line (larger by one degree than the morning hour angles). This lack of symmetry is due to systematic mistakes both in construction as well as the dial plate’s curved surface.
Other characteristic distances on the dial plate along the meridian line are from the top edge of the sundial to the curve of the winter solstice (1 cm), the lower edge of the gnomon’s base to the curve of the winter solstice (1cm) and from the curve of the summer solstice to the dial plate’s base (0.4 cm).
The hour angles generally show some symmetry regarding the meridian hour line, with the angles formed between the early morning hours being about one degree larger than those of the afternoon hours. This could be attributed to a construction error in the corresponding section of the dial plate and/or to a systematic error made while taking measurements.
This conical sundial with its gnomon is preserved in good condition and is the only one kept in the Archaeological Museum of Piraeus.
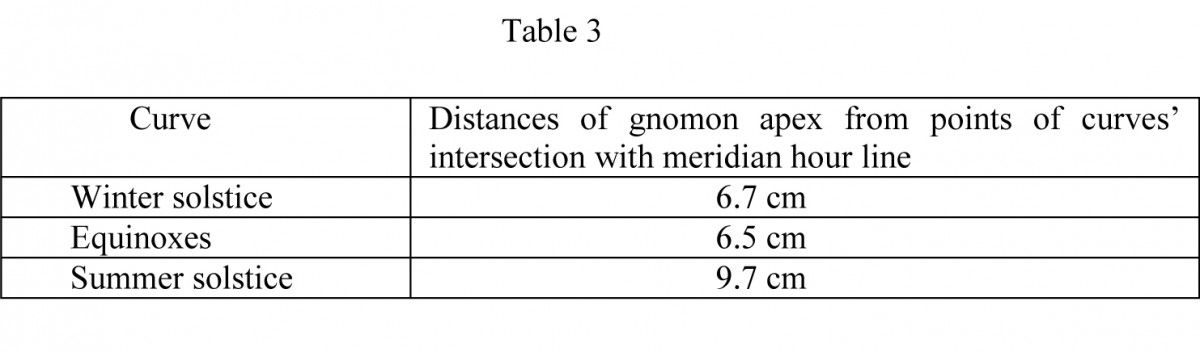
For the existing length of the gnomon (d=6.8 cm) a compass was used to measure the values of the distances between the intersection points of the curves with the meridian hour line from the gnomon’s apex, without taking into account the gnomon’s existing incline. They are listed in Table 3.
The values of the obliquity of the ecliptic (Table 4) were calculated by using the length of the hour line measured on the 6th (meridian) hour line between the curves (see Table 1) of the winter solstice and equinoxes (2.3 cm), as well as the equinoxes and summer solstice (5.5 cm).
Based on the sundial’s conical geometry we expected the resulting values of the ecliptic to be equal. There is a great difference between the two values, which can be attributed to an error in construction and /or a systematic error during the taking of measurements owing to the existing inclination of the gnomon. We observed that these values are quite different from the value of the obliquity of the ecliptic εtheoretical = 23ο 51΄26΄΄ = 23.86οas calculated by Eratosthenes (3rd century B.C.) (Pappus, Synagoge 546, 3- 550, 3, see also Jones 2002).
Values of this sundial’s characteristic parameters were calculated for each of those of the obliquity of the ecliptic (Table 5), namely the angle between the cone’s axis andρ the generator of the sundial surface, d the gnomon’s lengthand φ the geographic latitude.
We observed that for all the values of the obliquity of the ecliptic , the resulting length of the gnomon is around 4cm, which is considerably smaller than the length of the existing one (d = 6.8cm). Consequently the above experimental values of the obliquity of the ecliptic have been rejected. Nevertheless the same length of gnomon also results for the theoretical value of the obliquity of the ecliptic εtheoretical and therefore the topic needs further investigation.
For this reason it was considered necessary to calculate the gnomon’s initial length and the geographic operating latitude of the sun dial for the two experimental values of the obliquity of the ecliptic (ε1=19ο.99 and ε2=32ο.72).Resulting values for d the gnomon length and φthe geographic operating latitude are listed in Table 6, based on the geometry of conical sundials (see analytically Panou 2016: 192-200).
Furthermore with this methodology, the length of the gnomon, as calculated, is even smaller compared with the values listed in Table 5 and the operational latitude corresponds to regions in the greater area of Greece (the Northern Balkans).
Conclusions
To sum up all the above, we can conclude that the sundial was used in regions further north of northern Greece. The length of the sundial’s original gnomon was slightly more than half of the current one and consequently it can be established from both its slant and length that the gnomon was added subsequently.
We should note that this sundial was first described and its characteristic elements measured by Páris (1914: 121-130), who calculated the geographic operating latitude as φ= 36ο 36΄24΄΄ (a value close to the latitude of Piraeus φ= 37ο57′). He based this on calculations of the outer geometric features of the marble construction, rather than on measurements of the dial plate’s curves and hour lines. He also calculated the value of the obliquity of the ecliptic taking into account the geometric features of the curve of the winter and summer solstice as being ε = 24ο43΄22΄΄ and ε’ = 34ο43΄40΄΄respectively, which resulted in different values for the geographic latitudes and lead Paris to the conclusion that there were mistakes in the sundial’s construction.
Almost half a century later, this sundial was studied by Gibbs who calculated the following parameters as the value of the ecliptic ε = 24ο: namely ρ = 43ο20′; the angle between the cone and the generator,d = 4.68 cm; the length of the gnomon and φ = 35ο 12′; the geographical latitude. Moreover, taking into account the geometric features between the curve of the winter solstice and the equinoxes, she calculated the geographic operating latitude φχ= 26ο and respectively φs=13ο 24′ acknowledging the geographic characteristics between the curve of the equinoxes and that of the summer solstice (Gibbs 1976: 242). Owing to the sundial’s slanting gnomon, the results arrived at by Gibbs are of doubtful accuracy, since this problem is neither referred to nor does it seem to have been solved. We should not forget that Gibbs’ methodology in conical clocks is not applied in the case of sundials with a slanting gnomon. The last description was made by Schaldach (2006: 124), who places it in the category of conical sundials.
Evangelia C. Panou
Science Teacher in Secondary Education and PhD candidate in History and Philosophy of Natural Sciences at the University of Athens, Department of Physics
* Many thanks to archaeologist Mrs Angeliki Poulos, head of the Archaeological Museum of Piraeus and marble craftswoman Mrs Eleni Mazarakis for her help when measuring the characteristic features of the sundial.